没想到收到这么多赞。借着这个答案写一点题外话。因为这点题外话好懂,所以写在前面了。其实是两个话题,我写在自己的个人公众号里面了。除了写这个,我最近还写了一些关于古罗马历史的东西。小小的公众号求关注:younglings_2011
————————————————————————————————————————
我想在这里写写,我们是怎么适应了我们的宇宙,我们观察到的宇宙为什么是这个样子,最后说一点题外话。
初级版本
高中物理教材在讨论黑体辐射的时候,都是把太阳当做理想黑体的。太阳的温度是6000开尔文左右。太阳发出的光最大功率的频段就是可见光。有些宗教人士会说“这是上帝给人的恩惠”。其实是我们的眼睛为了适应太阳光而进化。因为太阳的温度是六千度左右,所以在某一频段上辐射的强度最大。而人类在昼间活动,自然要能看到最强的光线,也就是太阳光。
为什么25摄氏度是我们最舒服的温度,也不是什么上帝的恩惠,而是我们就是在这样的温度下进化而来。
远古的海洋盐度是0.9%,我们今天医院里用的生理盐水浓度也是0.9%。
知乎上有过一个很有趣的问题,为什么这个世界上没有哥斯拉那样可怕的巨兽?其实不是没有,而是我们人类就是。这个世界上绝大多数动物都是昆虫的大小,而在蚂蚁和蚂蚱面前,我们就是哥斯拉一样的存在。
我还真的想要讨论动物的大小问题。
在恐龙时代,不光恐龙长得那么巨大。白垩纪的蜻蜓也能长到一米长。我们知道,维持一个物体的形状不变,这个物体越大,表面积/体积的比值就越小,而对于生物体来说,这个比值太小,会导致生物体和外界物质交换困难。而所有的生物体,都需要排出废物,不断吸收营养。这也是为什么无论多大的生物,细胞只能长那么大。
对动物来说,想要得到足够的氧气。动物长得越大,就需要更大的肺。更大的肺,是指肺在身体中占据的比例也更大。
中生代的空气中,氧含量高达32%,而现在的空气中含氧量21%左右。所以中生代的空气足以支持恐龙那样的巨兽,今天的空气不能。
进阶版,进阶到真正物理的梗了呢。
真正物理的梗,我们观测到的宇宙为什么是这个样子的?
霍金在《果壳中的宇宙》里面讨论了几个很有趣的问题。其中一个就是“人存定理”,用我们的存在本身,来解释为什么我们观测到的宇宙是现在这个样子。因为只有在这样的宇宙中,我们才能生存,所以我们观察到的宇宙只能是这个样子。似乎能解释很多不好解释的问题:
为什么空间是三维的?或者说,为什么空间不是二维的?不能是四维甚至更高维度的?
二维的空间不足以容纳生命的复杂结构。霍金在《果壳中的宇宙》里面就给了一个例子:二维的骆驼。二维的骆驼怎么吃掉一个苹果?把自己分成两半吗?

为什么空间不能是四维甚至是更高维度的?
我们知道静电力和万有引力都是与距离的平方成反比的。我想这是因为我们生活在三维空间当中,而三维空间中存在着高斯定理。对电场来说,在一个封闭曲面上做对电场做积分,积分得到的通量和曲面内包含的电荷量成正比。而高斯定理使得这些力成为平方反比的作用力。
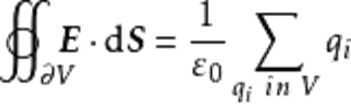
如果空间是四维的,电场力和万有引力想必会和距离的三次方成反比吧。三次方反比的结果,是电场力和万有引力的梯度太大,会撕裂我们所见的所有物体,就像土星撕裂土星环一样。
为什么土星环不能聚合成一颗真正的大卫星,而是只能形成一团尘埃和碎石漂在轨道上?土星环离土星太近了,它被土星引力的梯度撕裂,不能构成一个卫星。绝大多数星球都是靠引力来凝聚的。而在土星这样一个大家伙面前,土星环上的那些尘埃,不能靠自身的引力来对抗土星环的引力梯度,所以被撕裂。
在强大的引力梯度影响下,靠自身引力聚集已然不可能。所以只好靠分子间的作用力来聚合。可是聚合出来的东西,自然不会是那些大块头。毕竟只有引力的作用距离有那么远。

行星的引力梯度尚且如此,宇宙中最可怕的引力梯度就是黑洞。黑洞的引力梯度,大到可以撕裂比太阳大几百倍的恒星。

而真正接近黑洞的视界时,面对强大的引力,所有的物质结构都会被撕裂,包括我们刚刚说过的靠分子间作用力聚合的物体。即使是那些我们所以为牢不可破的结构,分子,原子,核子,那些我们所知道的最强的力:电磁力、强相互作用,面对真正的奇点,统统都是战五渣。
在四维的空间中,就会出现类似的问题。四维空间中,代入高斯定理,引力的表达式呈现三次方反比。而这个三次方反比的引力,无疑会有更大的梯度。这样引力梯度会撕裂我们。所以,我们不能生活在四维空间中。
霍金用人存定理解释的又一个问题是,为什么宇宙存在至今,是150亿年?
化学元素的产生,来源于大恒星内部的核聚变。碳、氧、氮,这些元素支撑着我们的生命。一颗大恒星从氢开始,在自身引力的作用下聚集,塌缩。在这一过程中,引力势能转化为这些氢分子的动能,也就是内能。内能不断积累,高温高压之下,氢聚变。聚变的结果,就是形成了更多更复杂的化学元素。
需要产生真正足够数量的重的化学元素,需要无数大恒星前仆后继地聚变,自然是需要更多的时间。
大恒星完成了它们的生命周期之后,这些化学元素在宇宙中游荡,重新在引力的作用下聚集,形成了像地球这样的行星。地球上无机物之间的化学反应,机缘巧合形成了有机物。有机物的化学反应更加复杂,慢慢出现了生命。一切等待都是那么漫长,150亿年之后,终于出现了我们人类这样的生命体。所以,我们观测到的宇宙是150亿年。


人存原理的逻辑是这样的:因为只有这样的世界能容纳我们,只有在这样的世界中我们才能存在,所以我们观察到的世界是这个样子的。
进阶+1版
万有引力是怎么产生的,有个很有趣的解释。
有个解释是,广义相对论所讲,物体的质量使空间弯曲。物体在空间中运动,而空间被庞大质量所扭曲,就出现了万有引力的效果。
然而我想讨论的是另一种解释。
两个物体,构成了一个势阱。根据不确定性原理,空间中波函数的位置和动量不能同时精确地测量。这个“不能精确测量”的意思,不是我们技术手段不够,而是说粒子和波的运动本身就是不确定的。势阱中的波函数不能是零。如果波函数是零的话,就违反了不确定性关系。所以,空间中的波函数一定是某一个基态。现在我改变两个物体之间的距离,也就改变了这个势阱。这个势阱中波函数的基态也就相应地改变,也就改变了波函数基态的能量。
物体的位移导致了能量的改变,这正是一个保守力的特征,所以万有引力诞生了。
终极版,接下来的内容是关于相对论的,可能对不懂物理的同学造成成吨伤害。
我直接略去了相对论发现的过程,感兴趣的亲们可以看霍金《果壳中的宇宙》第一章《相对论简史》;我也略去了相对论的公式推导,感兴趣的亲们可以去看大学物理教材。舒幼生《力学》北京大学出版社。这本书折磨了我一个学期之久。
其实为了写这一段,我确实花了一天时间从头到尾地推公式,然而我决定在这里把公式都略掉,毕竟我没在写教材。
狭义相对论中提出了不同于常识的时空变换:在不同的参考系下观测,时间和空间都会变化。洛伦茨变换引出了“动钟变慢”和“动尺收缩”的效应:如果一个物体,相对于我,以接近光速的速度在运动,我认为它的时间变慢了,我认为它的长度缩短了。
一个例子是来自宇宙射线中的μ子,在10-20km的高空中产生(大概是二次粒子吧)。实验测量之下,μ子的寿命(半衰期)大概是2.2μs( )。就算μ子用光速飞行,它们再衰变之前能走过的平均距离也只有0.66km。然而,我们在地面上就能观测到大量的μ子。
在μ子的参考系看来,地球在以接近光速运动,而动尺收缩效应,使得大气层变薄了。μ子认为自己并没有走10km,它走的距离还是0.66km。
在地球参考系看来,大气层还是那么厚。但是因为动钟变慢的效应,μ子的寿命大大延长了。也就是说,运动中的μ子寿命是远大于2.2μs的,μ子可以走完10km到达地球。
如果是一列火车,以接近光速的速度开进山洞呢?假设火车和山洞在静止时长度是相等的。那么在火车司机看来,山洞是运动的,所以缩短了,比火车短。在山洞门口的保安看来,火车是运动的,所以火车比山洞短。
现在保安做这样一件事情:在关上山洞后门的同时,打开山洞的前门。达到的效果就是,有那么一瞬间,火车是整个被关在山洞里面的。把火车关在山洞里面,就证明火车真的比山洞短了,对吗?然而在火车司机的参考系看来,火车还是比山洞长的,这怎么解释呢?
然而,在火车司机的视角来看,是山洞的前门先打开了,若干时间以后,山东的后门关上了。其实火车还是比山洞长的。
时间是什么?我们日常生活中对时间的测量,是基于对同时事件的观测。“两点钟我出门”也就是,钟的指针指向两点钟的时候,我出门了。但是我们用什么办法来对钟?我的意思是说,想要确定两件事情是“同时”,本身就很难。我们怎么知道时间?看表吗?但是看表的时候,信息也是以光速到了我的眼睛里啊。
对时间的测量,只有完全在同一地点,才是完全准确的。我在看表的过程中,“六点钟”这个信息以光速传递到我的眼睛里,这已经经历了一段时间。所以,这个测量其实是不严格的。
对距离的测量,只有同时测量,才是准确的。我测量一个桌子的长度,只有在t1时刻测量桌子的左边是x1, 右边是x2, 这样测出来的长度是准确的。如果我在t1时刻测量桌子左边x1,在t2时刻测量右边是x2,谁又知道这段时间里桌子动过没有呢?
洛伦茨变换本质上强调的是同时,同一地点的相对性:同时和同地的观测需要信息的传递,而信息的传递需要时间。因此,在不同的坐标系中,对不同的观察者而言,会出现不同的同时、同地标准。理解了这一层,就明白为什么长度和时间会随着坐标系的变换而改变。
洛伦茨变换的基础是:所有的参照系都是平等的,没有一个绝对静止的参照系;在各个参照系中,光速都是不变的。然后就是一系列推导了。
有了洛伦茨变换,动钟变慢和动尺收缩,就不难推导了。
想要测量时间,必须同地。想要测量空间,必须同时。而相对论对传统时空观真正的颠覆,就是提出在不同的参考系下“同时”和“同地”的标准都会变的。
而在刚刚山洞关火车的例子里:在火车司机的视角看来,保安测量火车长度这个行为并不同时,所以测量得不对。
相对论的另一个有趣的问题是双生子佯谬了。
双胞胎兄弟,一个留在地球上,一个坐着飞船去旅行。运动是相对的,所以在飞船上的哥哥看来,地球上弟弟的时间变慢了;在地球上的弟弟看来,飞船上的哥哥的时间变慢了。所以问题来了,哥哥和弟弟到底谁更年轻?
一直以来,很多人认为这个题目要诉诸广义相对论:哥哥在飞船上,要返回地球,要做加速运动。作加速运动的结果就是,他比弟弟更年轻。
在这里我想说的是,其实这个问题在狭义相对论的框架内就能解决。相对论的基本假设在于,在任何参考系中真空光速不变、两个事件之间的间隔不变。间隔的表示如下
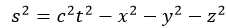
在我们平时对间隔的定义下,两点之间直线最短。然而在这个公式对“间隔”的定义之下,就成了两点之间直线最长。图中红线是坐飞船的哥哥在时空中的路线,蓝线是留在地球上的弟弟。
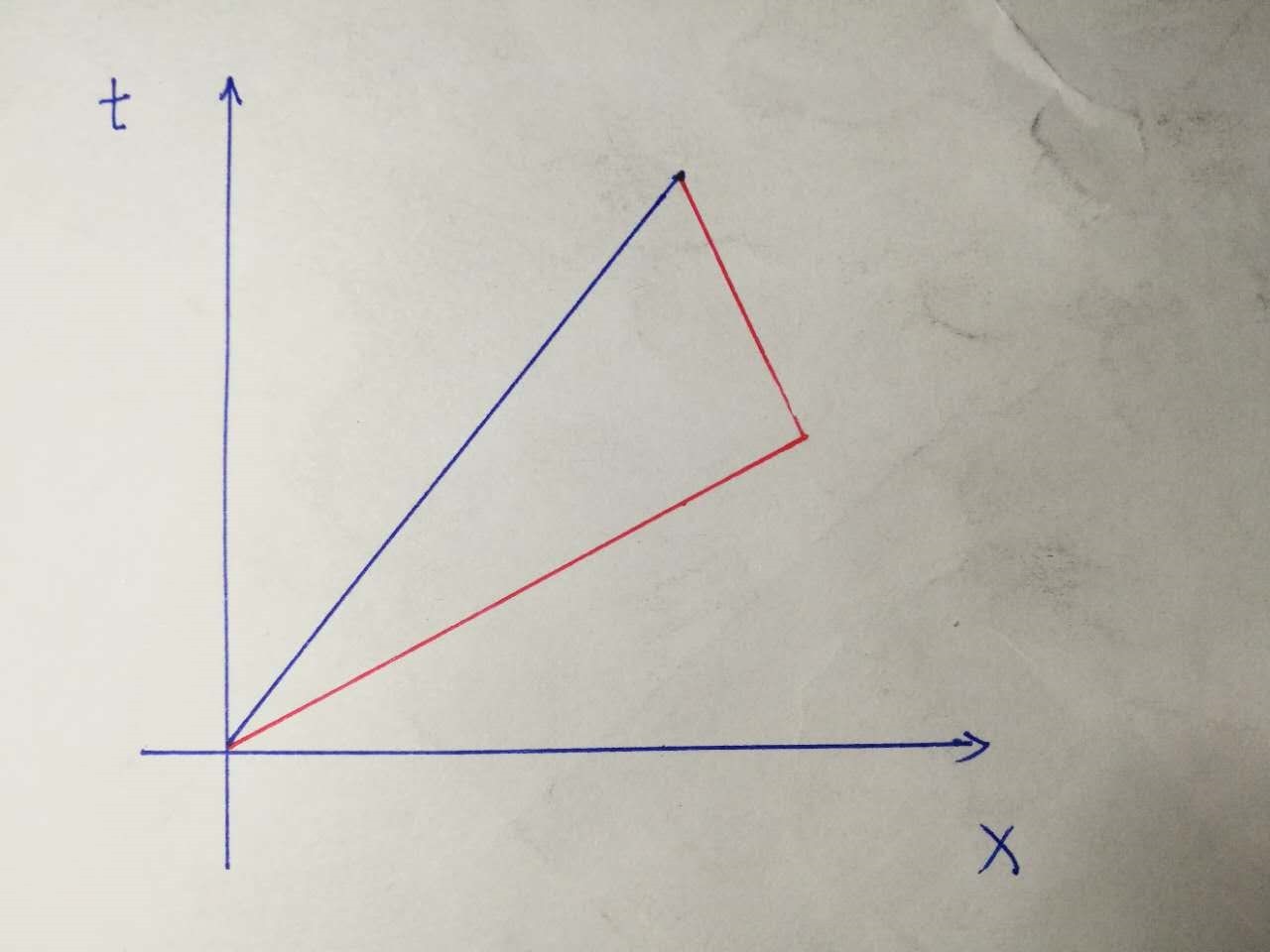
那么,不管哥哥飞出去多远,他想要回到地球跟弟弟比谁更老,都要走一条折线。两点之间直线最长,所以,弟弟走过的间隔线是比哥哥更长的。那么,这个问题的结论是:在任何一个参考系眼里,哥哥都比弟弟要年轻。
最后一个问题是爱因斯坦的那个著名的公式
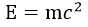
讲的是质量和能量的对应关系。这个公式到底是什么意思?我还特意讨教过好几个老师。答案是,其实在狭义相对论的语境之下,我们是不区分能量和质量的。质量就是能量,能量就是质量。就像我们在称体重的时候不会区分地球的重力和我们身体的质量一样。
质量守恒在相对论的语境之下,则表示动质量守恒。(洛伦茨变换的另一个结果,运动的物体质量会变大)而物体动质量与静止质量之差,就是它的动能了。 |