天体坐标系

炒股初哥春

在天文学和天体物理学中，从天文观测，到天体的运动，各种各样的坐标系总是离不开的一个话题。本章中，我将介绍天文学中几个常用的坐标系和坐标系之间的转换以及一些天文学知识。

• 地理坐标系 Geographic Coordinate System
  
• 地平坐标系 Horizonal Coordinate System
  
• 第一赤道坐标系（时角坐标系）First Equatorial System (HA-dec)
  
• 第二赤道坐标系 Second Equatorial System (RA-dec）
  
• 黄道坐标系 Ecliptic Coordinate System
  
• 坐标系转换 Transformation of Coordinate
  
• 中天 Culmination
  
• 太阳 Sun
  

地理坐标系 Geographic Coordinate System

地理坐标系就是我们在生活中最常见的坐标系，是由纬度、经度和相对于地面的高度所组成的三维球面坐标系。通过经纬度和相对于地面的高度，我们就可以表示和定位地球上任意一点的坐标。
在地理坐标系中，基本的方向为地球自转轴，地球自转轴的两端分别为北天极和南天极，和地球自转轴垂直的最大平面为赤道（Equator），穿过北天极和南天极的大圆都被称为子午线/经线（Meridian）。



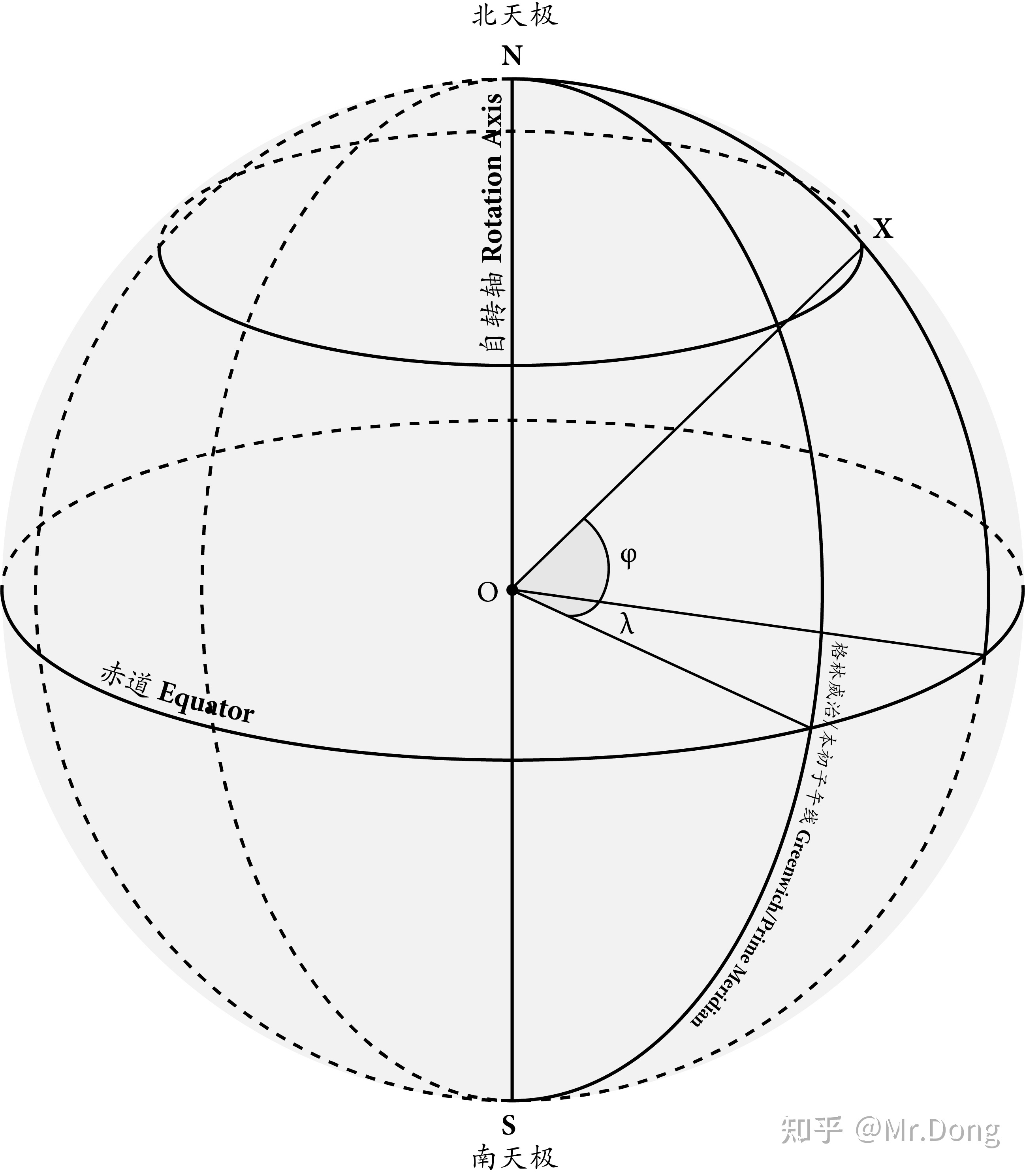
地理坐标系 Geographic coordinate System

把点O看作地心，图中x的坐标可以用3个参数来表示：

• 纬度φ：赤道面与过XO的直线所组成的夹角（线面角）；
  
• 经度λ：过点X的子午线/经线和格林威治/本初子午线之间的夹角（两面角）;
  
• 高度h：即X相对于海平面的垂直距离；
  

格林威治/本初子午线（Greenwich Meridian/Prime Meridian）是指经过伦敦格林威治天文台的子午线。格林尼治东面和西面的经度分别用x°“E”和x°“W”表示，比如北京天安门的经度就是116°24' E 。
对于观察者来说，其所能看到的天空取决于它的地理位置。当经度改变时，星体的中天（Culmination）（天体经过当地子午线的时刻）、升起和落下的时刻都会发生变化；地球的自转速度大概为每小时15°，也就是说，如果一个星体在晚上8点在北京（经度116°）升起，那么你在青海西宁（经度101°）就要一个小时之后才能看到这颗星体升起。
纬度会改变星体在视线中的位置和时间，比如在赤道上，所有的星体都会升起和降落，在南北极，只有一半的星体可见，并且所有可见的星体都为拱极星（Circumpolar Star * 具体会在后面的章节介绍），在其余的地区，有些星体可见，有些为拱极星，有些会永远在视线之外。



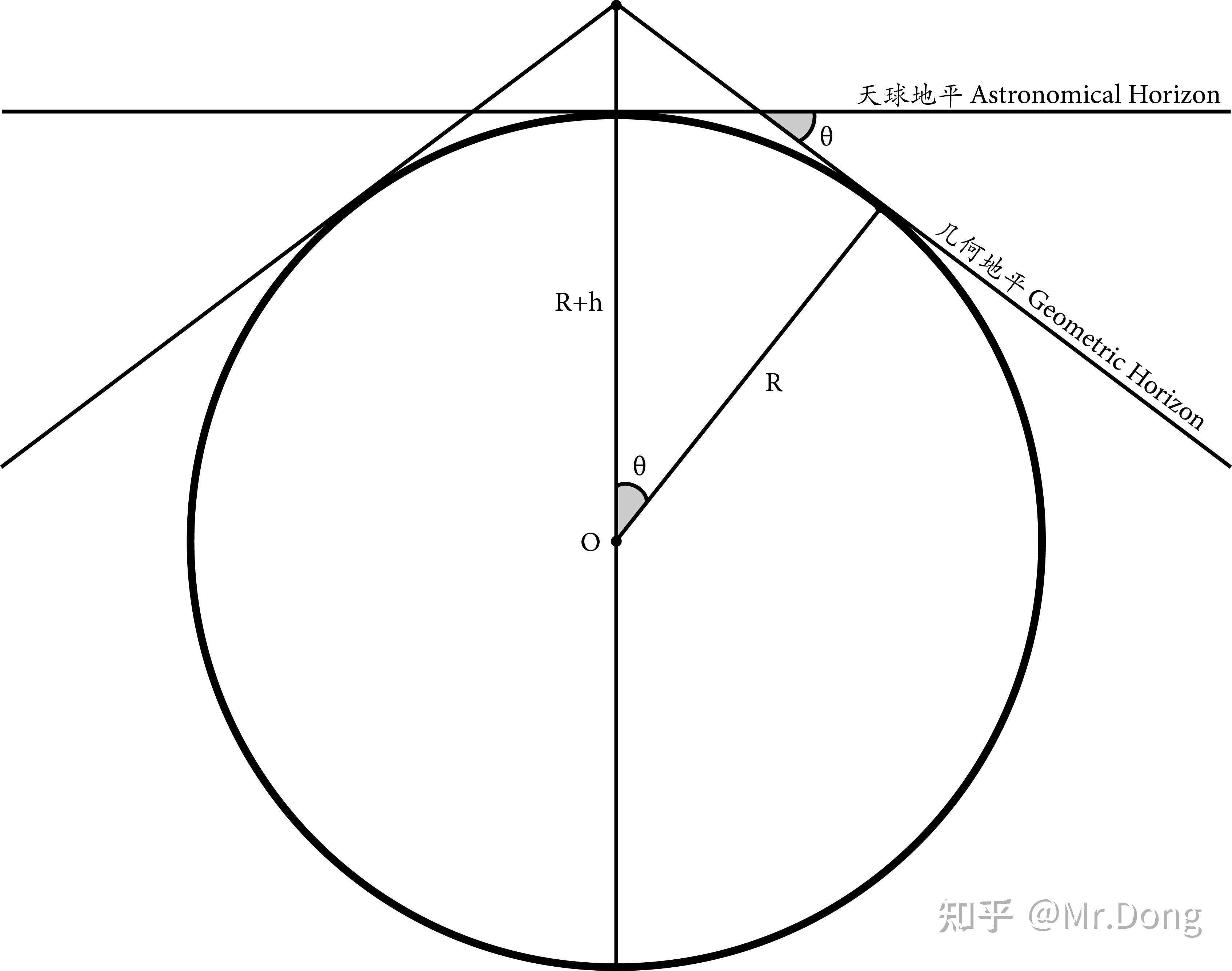
天球地平和几何地平

相对于地面的高度决定了视野的大小，从上图中可以看出，如果你站在一个高楼上面，那么你的几何地平（Geometric Horizon）或者视地平（Apparent Horizon）就会比在平面上多出2θ的视野。
θ的计算也非常的简单：
(R+h)\cos\theta=R\\ \boxed{\theta=\arccos(\frac{R}{R+h})}\\
在之后的章节中，相对于地面的高度统一为0，如果需要计算的话仅仅需要在原有角度上加上增加的θ就可以了。
<hr/>地平坐标系 Horizonal Coordinate System

地平坐标系是天文学中非常重要的坐标系之一，它以观测者所处的位置为中心，并且将观测者的视线作为基本面，也就是地平圈。地平圈具体的定义就是和铅垂线垂直的平面并和天球相切，也就是我们所说的天球地平（Astronomical Horizon）。



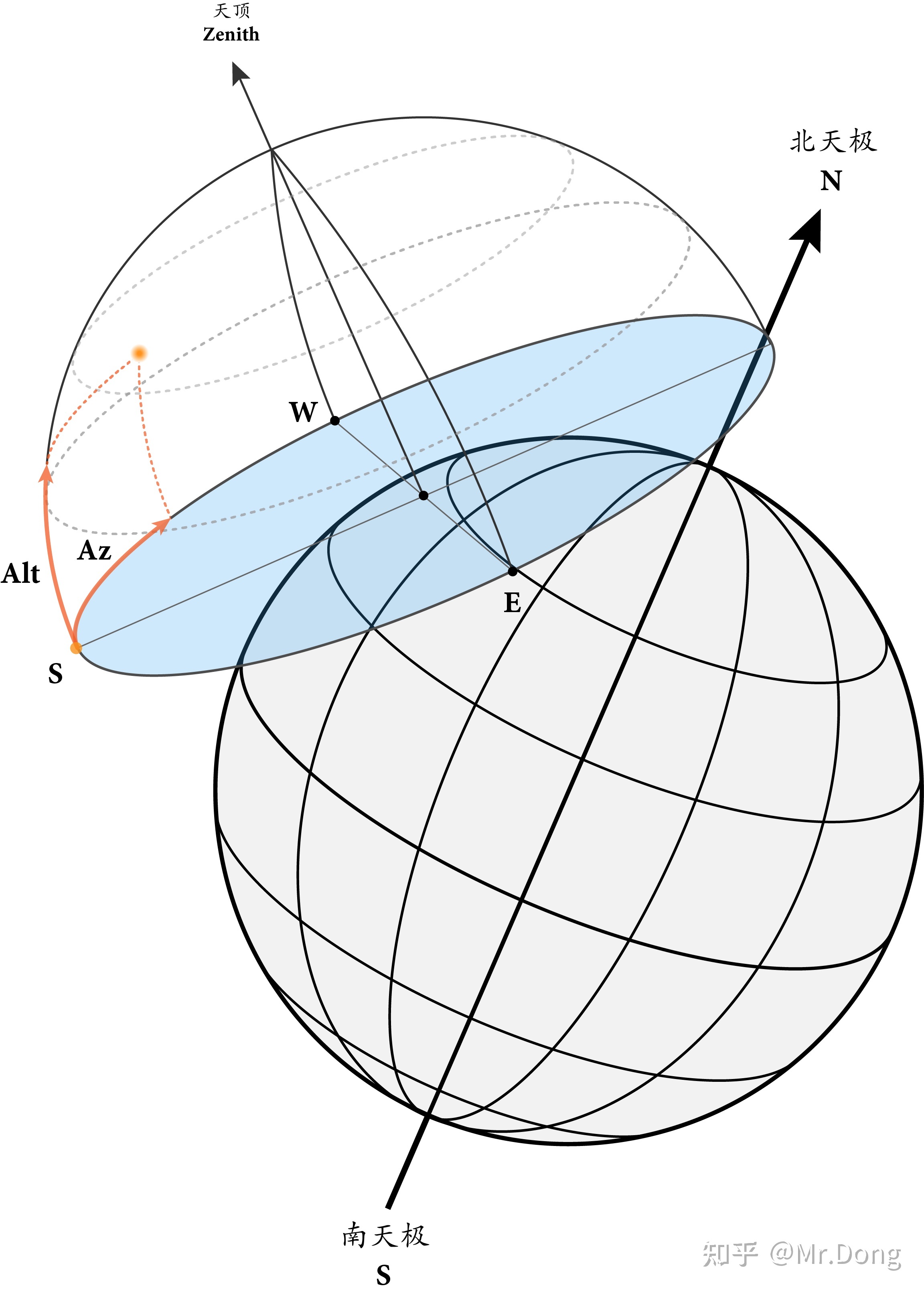
地平坐标系 Horizontal Coordinate System - 图1

地平坐标系将天空分为了两个半球，在上半球或者地平线以上的天体，我们都可以观测到；但是因为地球的遮挡，所以我们无法观测到在下半球的天体。天顶（Zenith）和天底（Nadir）是铅垂线和天球相交的相交点，天顶在上半球，天底在下半球。
所有通过天顶和天底的大圆被称为地平经圈（Vertical），与地平圈平行的小圆被称为地平纬圈（Almucantar）。通过地球自转轴或者北天极和南天极的地平经圈被称作天球子午圈（Principal Vertical），天球子午圈和地平圈的相交点就被定义为地平坐标系中的北点和南点，和天球子午圈垂直的地平经圈被称为卯酉圈（Prime Vertical），并且将它与地平圈相交于定义为东点和西点。



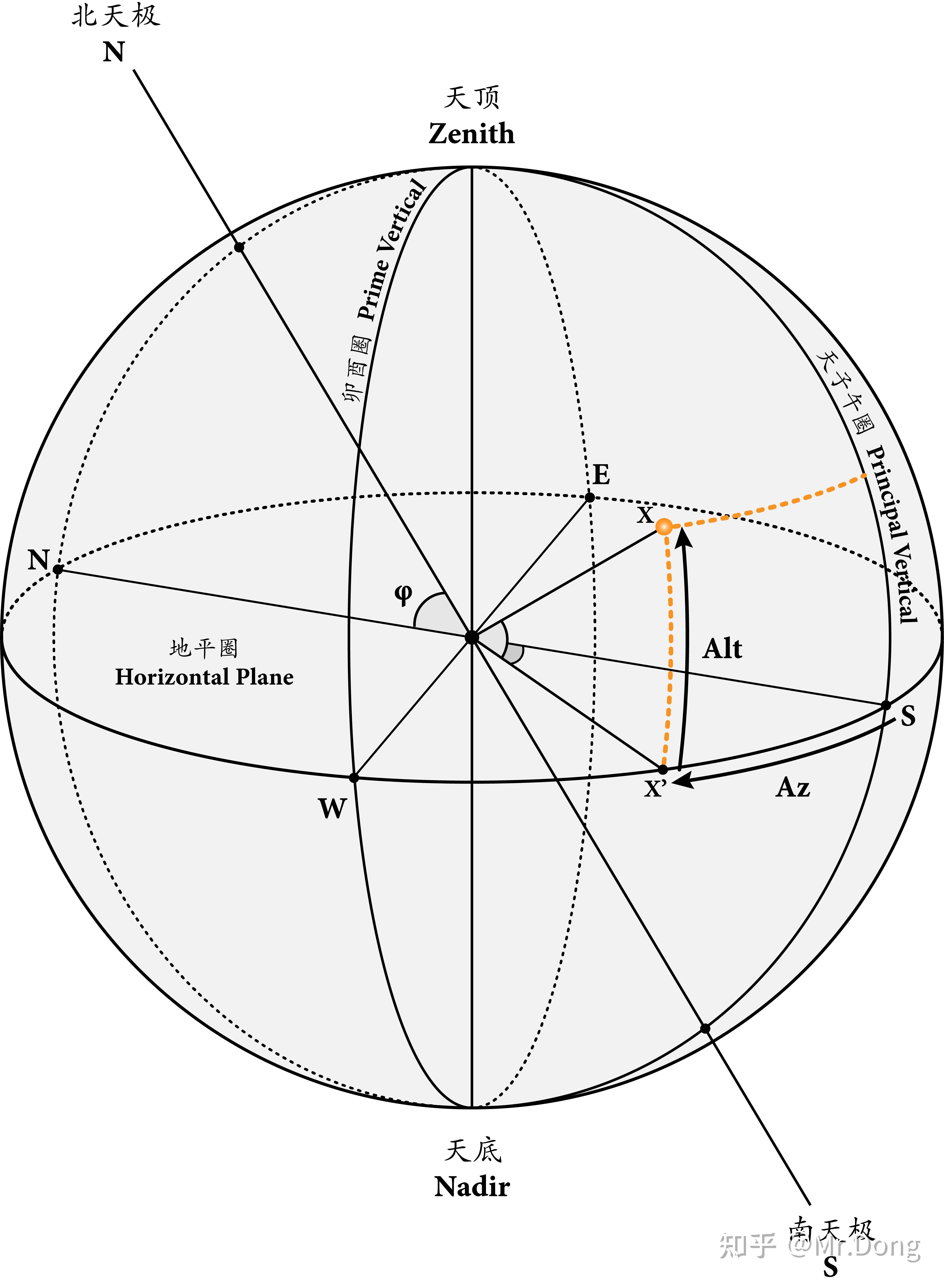
地平坐标系 Horizontal Coordinate System - 图2

如图2所示，X为一个在天球中的星体的坐标，并且 X' 为X在地平圈上的投影。那么X在地平坐标系中的坐标就可以用一下2个参数来定义：

• 方位（Azimuth），即地平经度，简称Az，；也就是角 SX'，即天子午圈与天体所在的地平经圈平面的夹角（ 两面角），从南点（S）以顺时针方向测量。方位角的取值范围为0°～360°。
  
• 高度（Altitude），即地平纬度，简称 h 或 Alt ; 也就是角 XX' , 即天体和观测者的连线与地平圈的夹角（线面角）或者天体的仰视角。高度的取值范围为+90° ~ -90°， 当高度为正数时，天体位于地平圈以上，也就是可见的天体，当高度为负数时，天体位于地平圈以下，也就无法观测。
  

天体的高度和方位可以用经纬仪直接测出，也可以用量角器大致估量。
*图中角度φ指的是地理坐标系中的纬度φ
第一赤道坐标系（时角坐标系）First Equatorial System (HA-dec)

第一赤道坐标系或时角坐标系和之后要介绍的第二赤道坐标系一样，都是以天赤道（地球赤道平面延伸后与天球相交的大圆）为基本面并且以地球自转轴为基本轴的天球坐标系。唯一不同的是，第一赤道坐标系的第二坐标-时角H是和观察者所处的经度和时间相关的，第二赤道坐标系的第二坐标-赤经是和时间和观察者的地理位置无关的。



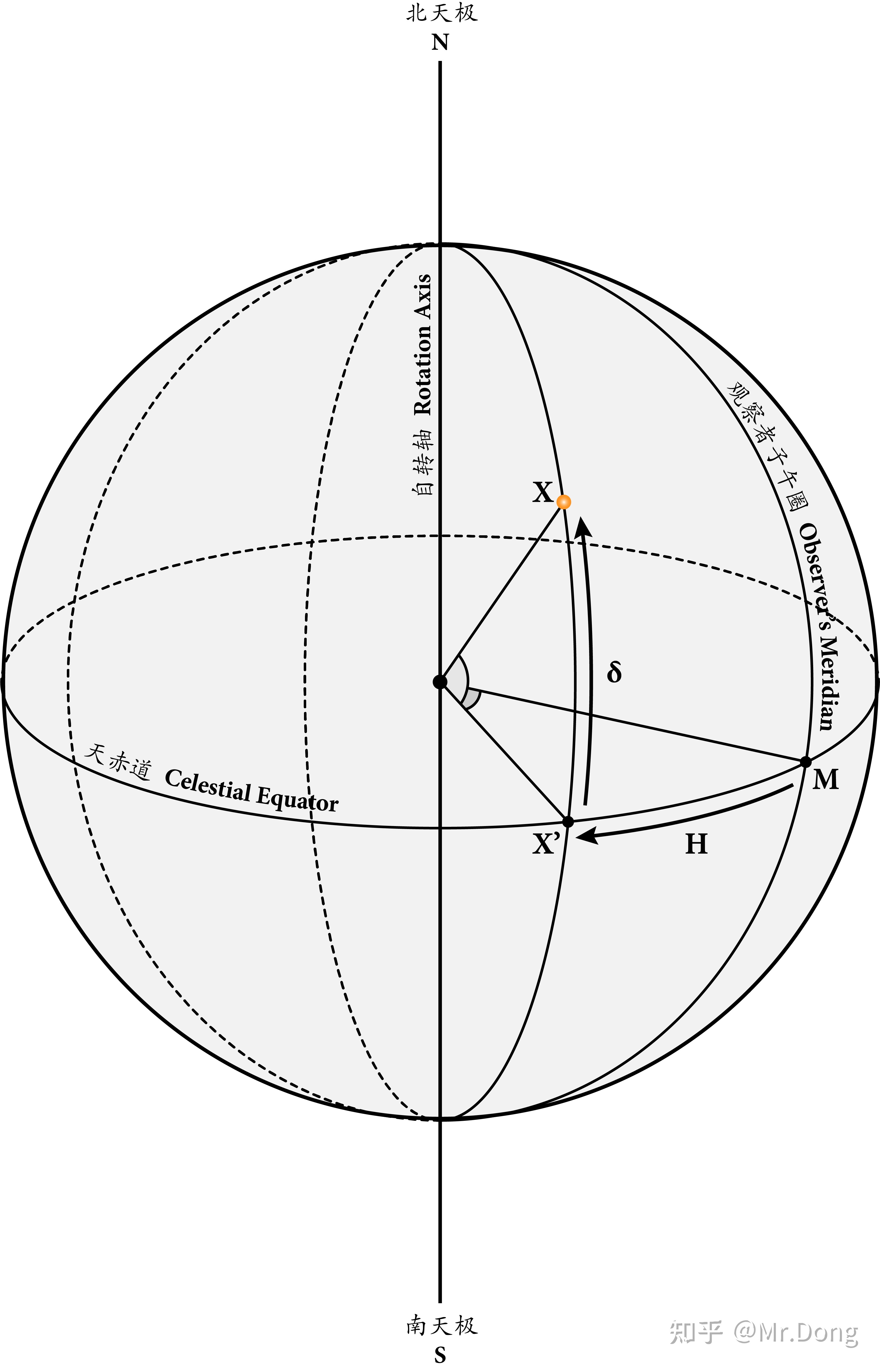
时角坐标系 HA-dec Coordinate System

让X为一个在天球中的星体的坐标，并且 X' 为X在赤道面上的投影。那么X在第一赤道坐标系中的坐标就可以用一下2个参数来定义：

• 时角（Hour Angle）,简称H；也就是角 MX'，即天体所处的子午圈和观察者所处的子午圈所形成的夹角；从观测者所处子午圈起向西（顺时针方向）测量，取值范围以小时为单位从0h - 24h， 每15° 为1h，（有时也可以用角度表示）。
  
• 赤纬（Declination），简称δ；也就是角 XX'，即天体和地心的连线与赤道面的夹角（线面角） ，取值范围为+90° ~ -90°，+90度为北天极，-90度为南天极，如果天体位于北半球，那么其赤纬就是正数，相反，如果天体为于南半球，那么赤纬就是负数。
  

*此图中的星体X和上面图中的星体X的位置可能有差距
在时角坐标系中，由于地球的自转，星体的时角会随着时间匀速增加（假设赤纬不变）。



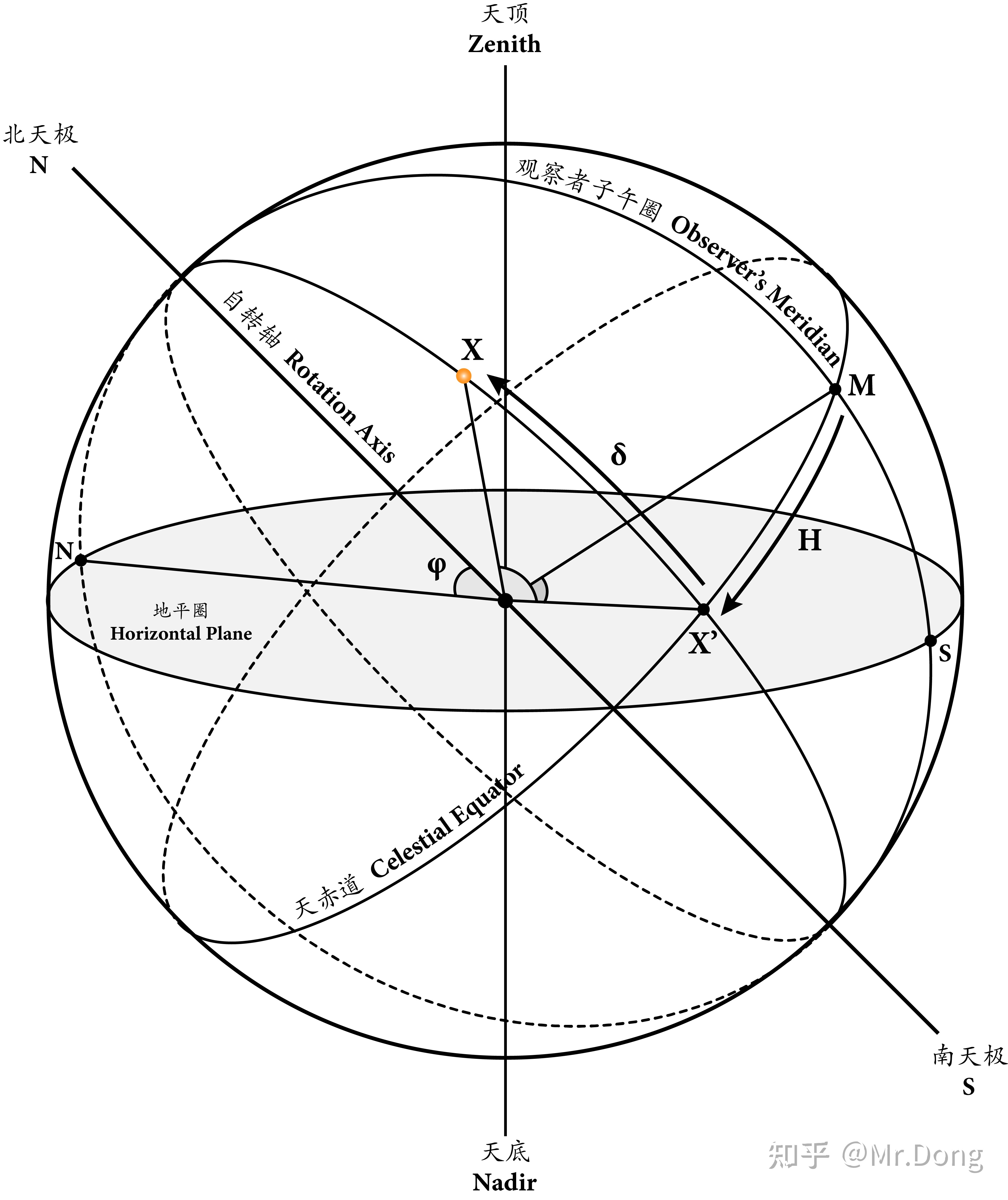
地平坐标系和第一赤道坐标系

上图中展示了一个处于纬度φ的观测者使用第一赤道坐标系所表示的星体，由于天球的半径可以是任意长的，所以地球的半径相比而言就会很小。因此，观测者所在的点可以被认为是与地心重合的，同样的，地心也可以被看做为地平圈的圆心。
<hr/>第二赤道坐标系 Second Equatorial System (RA-dec)

由于地球的自转，一个天体的时角是一直随着时间所变化的，除此之外，在不同的地理位置中，由于所处的经度不同，那么其时角也是不同的。所以，我们还需要另外一个与时间无关坐标系-第二赤道坐标系（RA-dec）。
在介绍坐标之前，先来介绍一下在第二赤道坐标系中非常重要的两个点-春分（Vernal Equinox）和秋分（Autumnal Equinox）：

• 春分和秋分都是中国二十四节气中的两个非常重要的节气，白昼和黑夜将会在这两天中平分，也就是说，白昼和黑夜的时间会各为12小时；在这两天中，太阳将会经过天赤道，也就是说太阳的赤纬将会是0°。在春分之后，太阳的赤纬会逐渐增加（直到夏至），北半球各地白昼开始长于黑夜；在秋分之后，太阳的赤纬会逐渐减少（直到冬至），北半球各地白昼将会短于黑夜。
  
• 太阳、月亮或者太阳系中的其他行星，其轨道非常接近黄道面（Ecliptic Plane），并倾向于将地球的赤道拉向黄道面。因为这种影响，地球就会像陀螺一样绕着垂直于黄道的轴线旋转，地轴的轨迹就形成了一对圆锥体，周期为25765年，这个移动叫做岁差（Precession）。因为这个原因，春分和秋分点每年会移动50"24 ，并且星表都会在每个世纪中更新；最近的星图和星表都是指星体在J2000.0（2000年1月1日）时的坐标。
  
• 在古希腊时期，春分和秋分会发生在太阳分别位于白羊座和天秤座的时候，因此，春分点会被表示为白羊座的符号，秋分点会被表示为天秤座的符号（因为在ai中打不出这些符号，所以我用V和A替换了这两个符号）。由于岁差的原因，现在太阳经过天赤道的时间晚了大概一个月，也就是一个星座，所以现在太阳在春分和秋分时分别位于双鱼座和处女座。
  

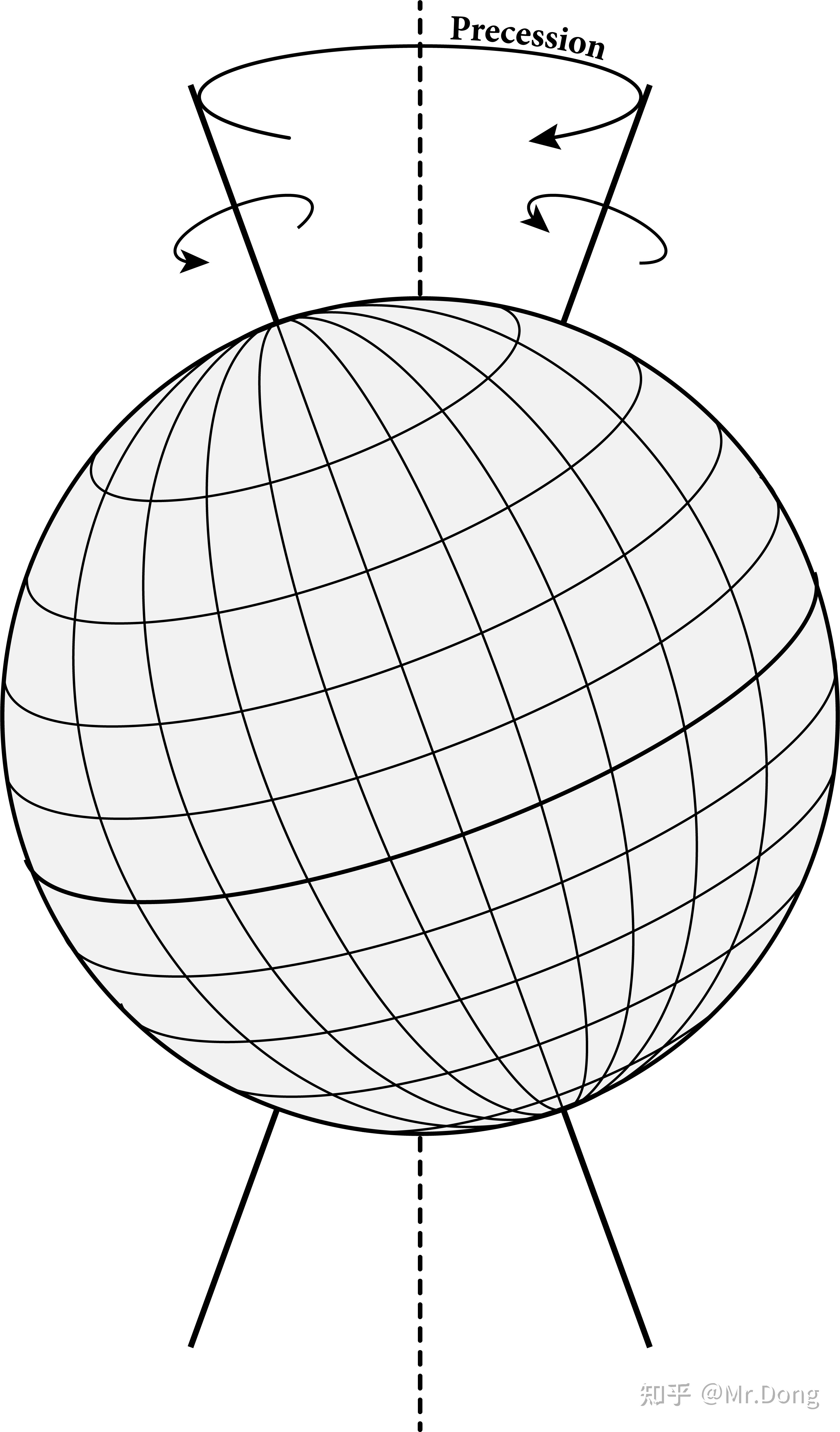
岁差Precession



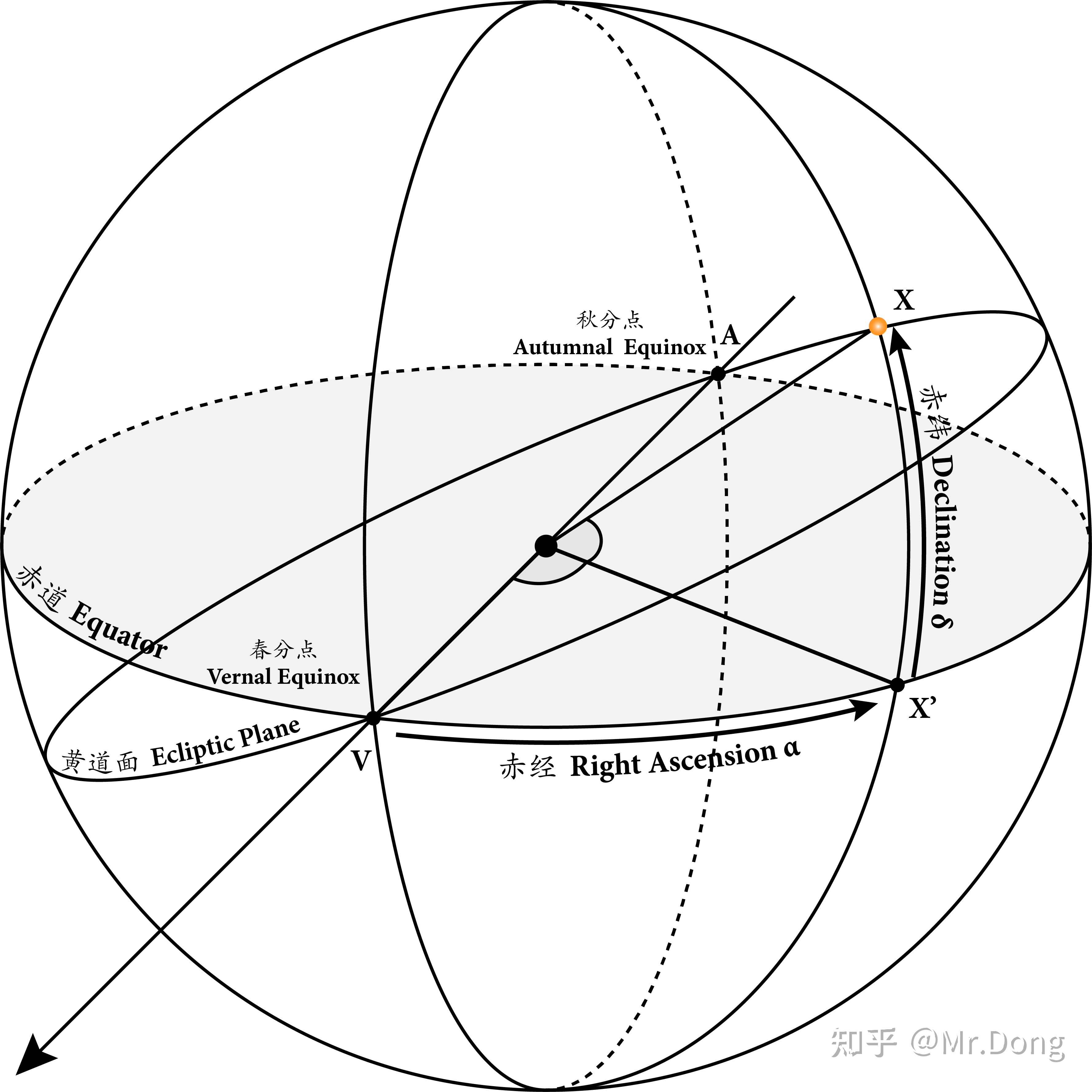
第二赤道坐标系 RA-dec

还是和原来一样，将X设为一个在天球中的星体的坐标，并且 X' 为X在赤道圈上的投影。那么X在第二赤道坐标系中的坐标就可以用一下2个参数来定义：

• 赤经（Right Ascension），简称α；也就是角VX'，从春分点开始向逆时针方向测量，取值范围以小时为单位从0h - 24h， 每15° 为1h，（有时也可以用角度表示）。
  
• 赤纬（Declination），简称δ；也就是角 XX'，即天体和地心的连线与赤道面的夹角（线面角） ，取值范围为+90° ~ -90°。
  

<hr/>黄道坐标系 Ecliptic Coordinate System

黄道坐标系是以黄道面为基本面并且以春分点为原点组成的天球坐标系。和第二赤道坐标系一样，黄道坐标系的坐标不会随着时间或者观察者的地理位置而变化。



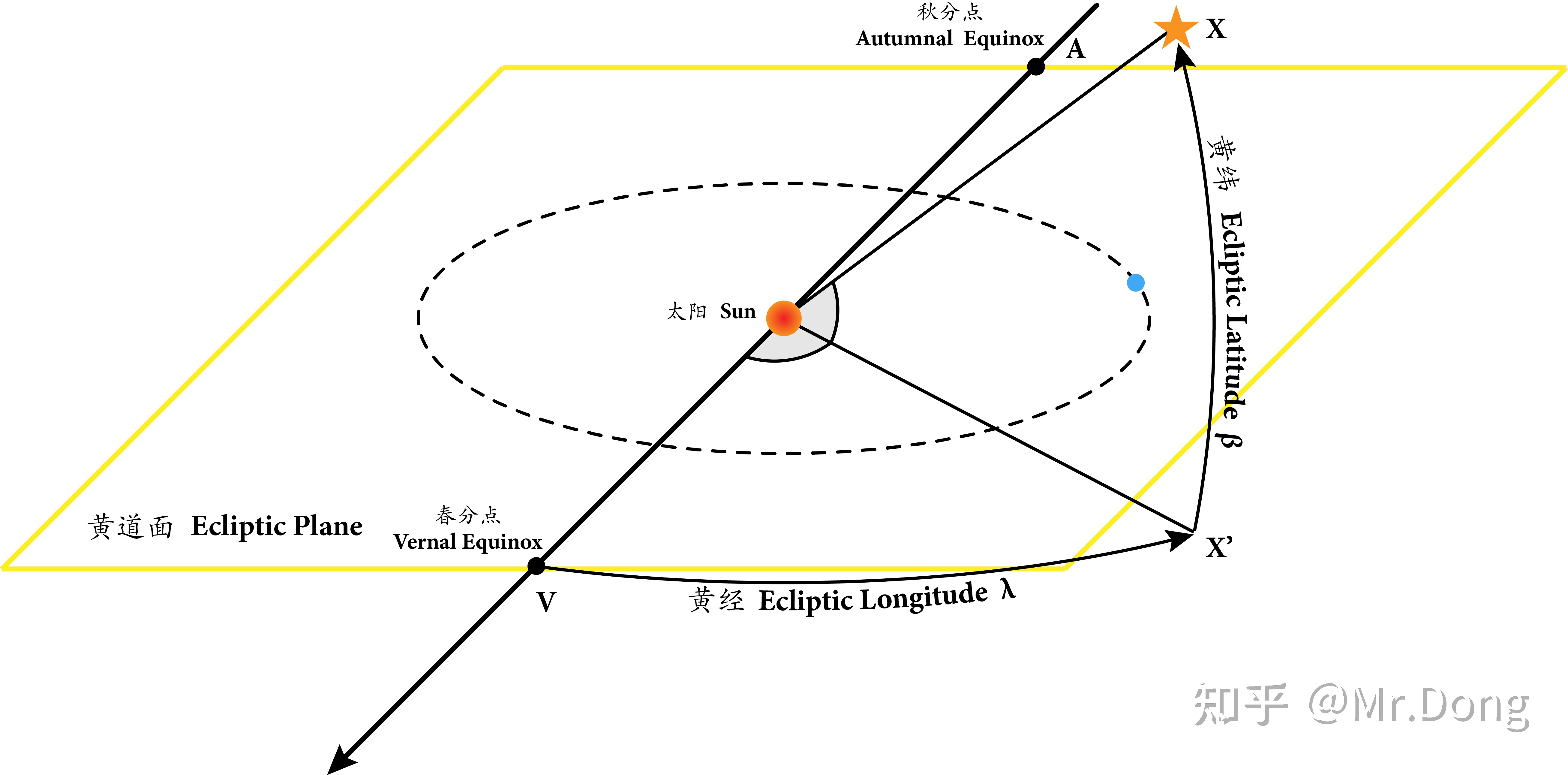
黄道坐标系 Ecliptic Coordinate System

将X设为一个在天球中的星体的坐标，并且 X' 为X在黄道面上的投影。那么X在黄道坐标系中的坐标就可以用一下2个参数来定义：

• 黄经（Ecliptic Longitude），简称λ；也就是角VX'，从春分点开始向逆时针方向测量，取值范围为 0° ~ 360°。
  
• 黄纬（Ecliptic Latitude），简称β；也就是角 XX'，即天体和太阳的连线与黄道面的夹角（线面角） ，取值范围为+90° ~ -90°。
  

• 因为岁差，每个星体的黄经每年移动50"
  

<hr/>坐标系转换 Transformation of Coordinates

在天文学中，坐标系的转换总是离不开的一个话题；比如，在星表中的星体的坐标通常是用第二赤道坐标系来表示的，所以如果你想要找到这颗星体，就需要将第二赤道坐标系转化成地平坐标系。



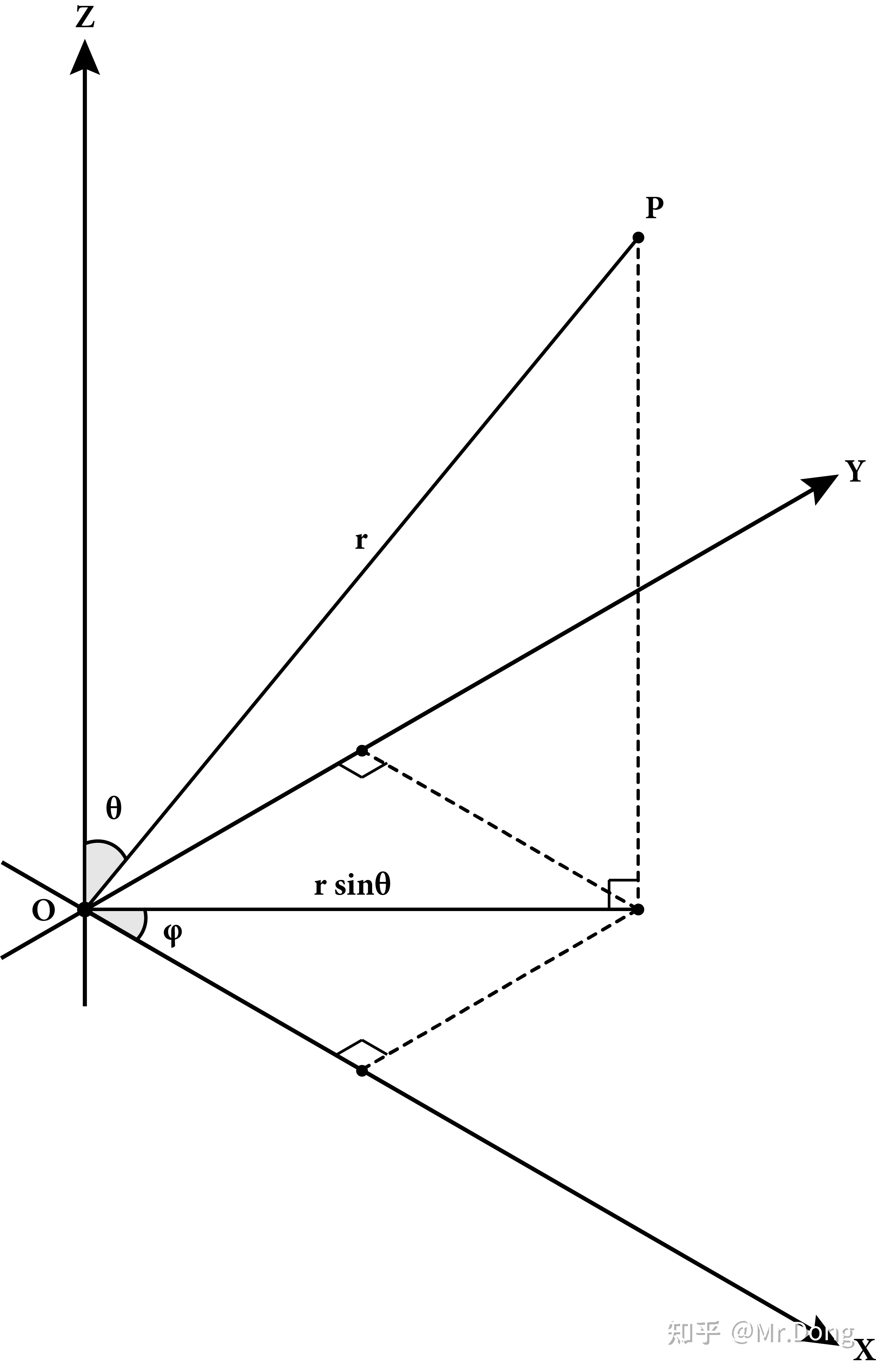
物理学中常用的球极坐标系 Spherical coordinates (r, θ, φ) as commonly used in physics (ISO 80000-2:2019）

在天文学中坐标系和我们常用的卡迪尔坐标系不同，卡迪尔坐标系将一个点的坐标用（x,y,z）三个坐标来表示，而天文学中的坐标系都会使用球中的角度来定义一个坐标，也就是所谓的球极坐标系。球极坐标系中的点会使用2个角度和距离原点的位置来定义；如上图所示，r为点P和原点的距离，第一个角θ为r和Z轴的角度，第二个角φ为r在xy平面上的投影和X轴形成的角度(逆时针)。
之后，我们将卡迪尔坐标系中的x,y,z转换成r,θ,φ
\begin{eqnarray}   \begin{cases} x=r\cos\phi\,\sin\theta & \tag{1}\\ y=r\sin\phi\,\sin\theta &  \\ z=r\cos\theta&\\   \end{cases} \end{eqnarray}\\   
另外一个坐标系中的x',y',z'写成，（将r设为1）
\begin{eqnarray}   \begin{cases} x'=\cos\phi'\,\sin\theta' & \\ y'=\sin\phi'\,\sin\theta' &\\ z'=\cos\theta'&\\   \end{cases} \end{eqnarray}\tag2\\   


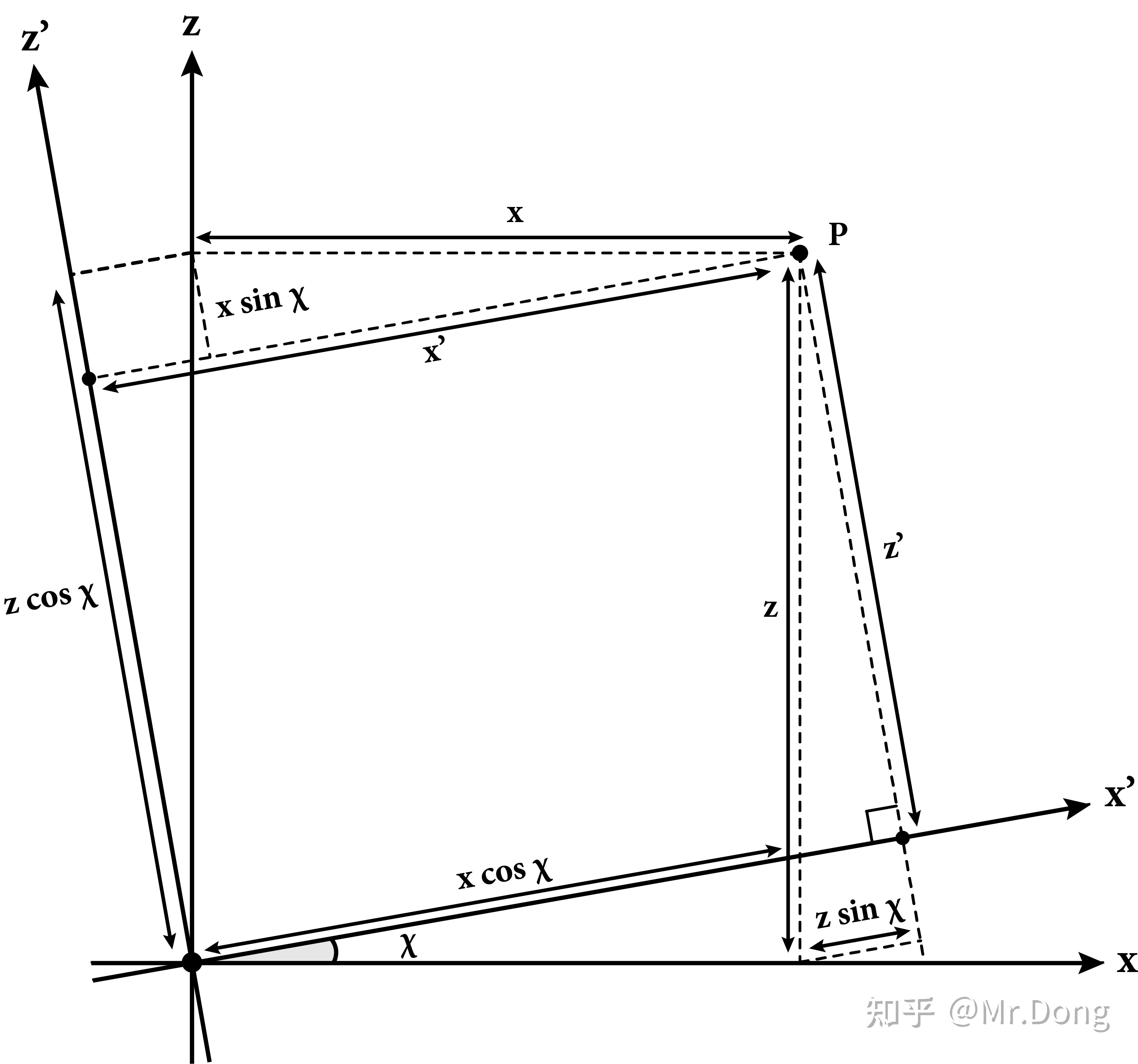
如果我们现在将xyz坐标系沿y轴旋转一个角度χ得到x'y'z'
现在我们用x,y,z和旋转的角度χ表示x',y',z',
\begin{eqnarray}   \begin{cases} x'=x\cos\chi + z\sin\chi & \\ y'=y&\\ z'=z\cos\chi-x\sin\chi &\\   \end{cases} \end{eqnarray}\tag3\\   
之后将方程1和方程2中代入方程3（将r设为1）：
\begin{eqnarray}   \begin{cases}  \cos\phi'\sin\theta'= \cos\phi\sin\theta\cos\chi+\cos\theta\sin\chi & \\  \sin\phi'\sin \theta'=\sin\phi\,\sin\theta &\\  \cos\theta'=\cos\theta\cos\chi-\cos\phi\sin\theta\sin\chi\\   \end{cases} \end{eqnarray}\tag4\\   
有了这三个方程，在所有的坐标系转换中，我们需要做的仅仅是将对应的角找到
地平坐标系到时角坐标系




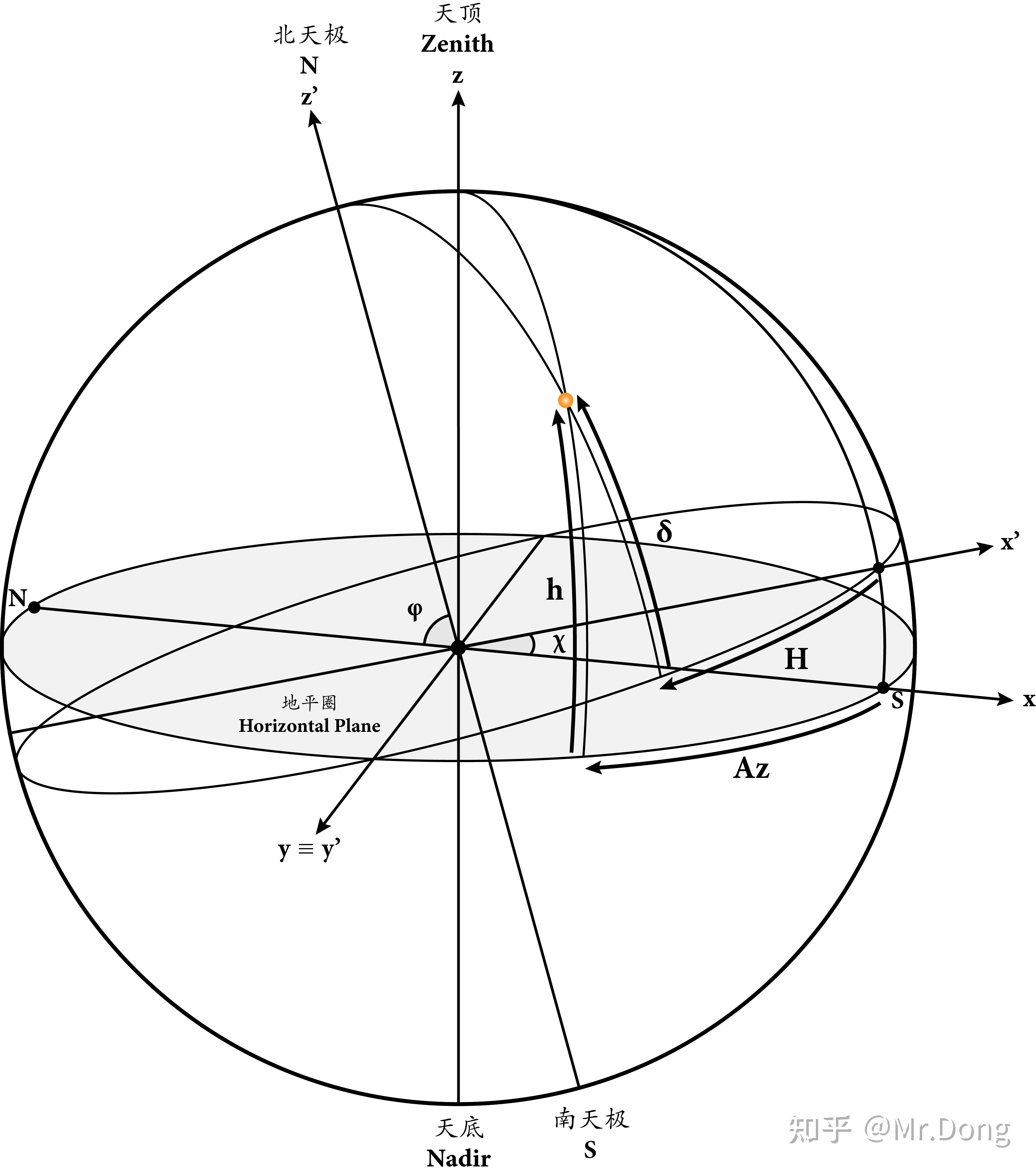
地平坐标系到时角坐标系

我们现在将地平坐标系中Az,h和时角坐标系中的H,δ和纬度φ与方程4中的ψ,ψ',θ,θ',χ一一对应起来（*由于方程4中的φ和纬度φ使用的是同一个拉丁字符，所以为了避免歧义，方程4中的φ用ψ代替）
\begin{eqnarray}   \begin{cases}  \psi = - Az & \\  \psi' = -H &\\ \theta = 90^\circ - h &\\  \theta' = 90^\circ - \delta&\\ \chi = 90^\circ - \phi&\\  \end{cases} \end{eqnarray}\tag{5.1}\\   
由于ψ的角度是以逆时针来测量的，所以ψ和ψ'分别等于-Az和-H；θ是从z轴开始的角度，所以θ,θ'和h,δ分别互为余角，最后两个基本面之间所旋转的角度χ就是90°-φ，之后我们将对应的关系代入方程4：
\begin{eqnarray}   \begin{cases}  \cos-H\sin(90^\circ-\delta)= \cos-Az\sin(90^\circ-h)\cos(90-\phi)+\cos(90^\circ-h)\sin(90^\circ-\phi) & \\  \sin(-H)\sin(90^\circ-\delta)=\sin(-Az)\sin(90^\circ-h) &\\  \cos(90^\circ-\delta)=\cos(90^\circ-h)\cos(90^\circ-\phi)-\cos(-Az)\sin(90^\circ-h)\sin(90^\circ-\phi)\\   \end{cases} \end{eqnarray}\\   
化简得：
\begin{eqnarray}   \begin{cases}  \cos H\cos\delta= \cos Az\cos h\sin\phi+\sin h\cos\phi & \\  \sin H\cos\delta=\sin Az\cos h &\\  \sin\delta=\sin h\sin\phi-\cos Az\cos h\cos\phi\\   \end{cases} \end{eqnarray}\tag{5.2}\\   
如果需要将时角坐标系转换为地平坐标系只需要将Az,H和h,δ相互调换并且将χ的符号变换一下即可：
\begin{eqnarray}   \begin{cases}  \psi = - H & \\  \psi' = -Az &\\ \theta = 90^\circ - \delta &\\  \theta' = 90^\circ - h&\\ \chi = - (90^\circ - \phi)&\\  \end{cases} \end{eqnarray}\tag{6.1}\\   
代入方程4：
\begin{eqnarray}   \begin{cases}  \cos Az\cosh= \cos H\cos \delta\sin\phi-\sin\delta\cos\phi & \\  \sin Az\cos h=\sin H\cos \delta &\\  \sin h=\sin\delta\sin\phi+\cos H\cos \delta\cos\phi\\   \end{cases} \end{eqnarray}\tag{6.2}\\   
注意和方程5.2的的符号有些差别

黄道坐标系到第二赤道坐标系




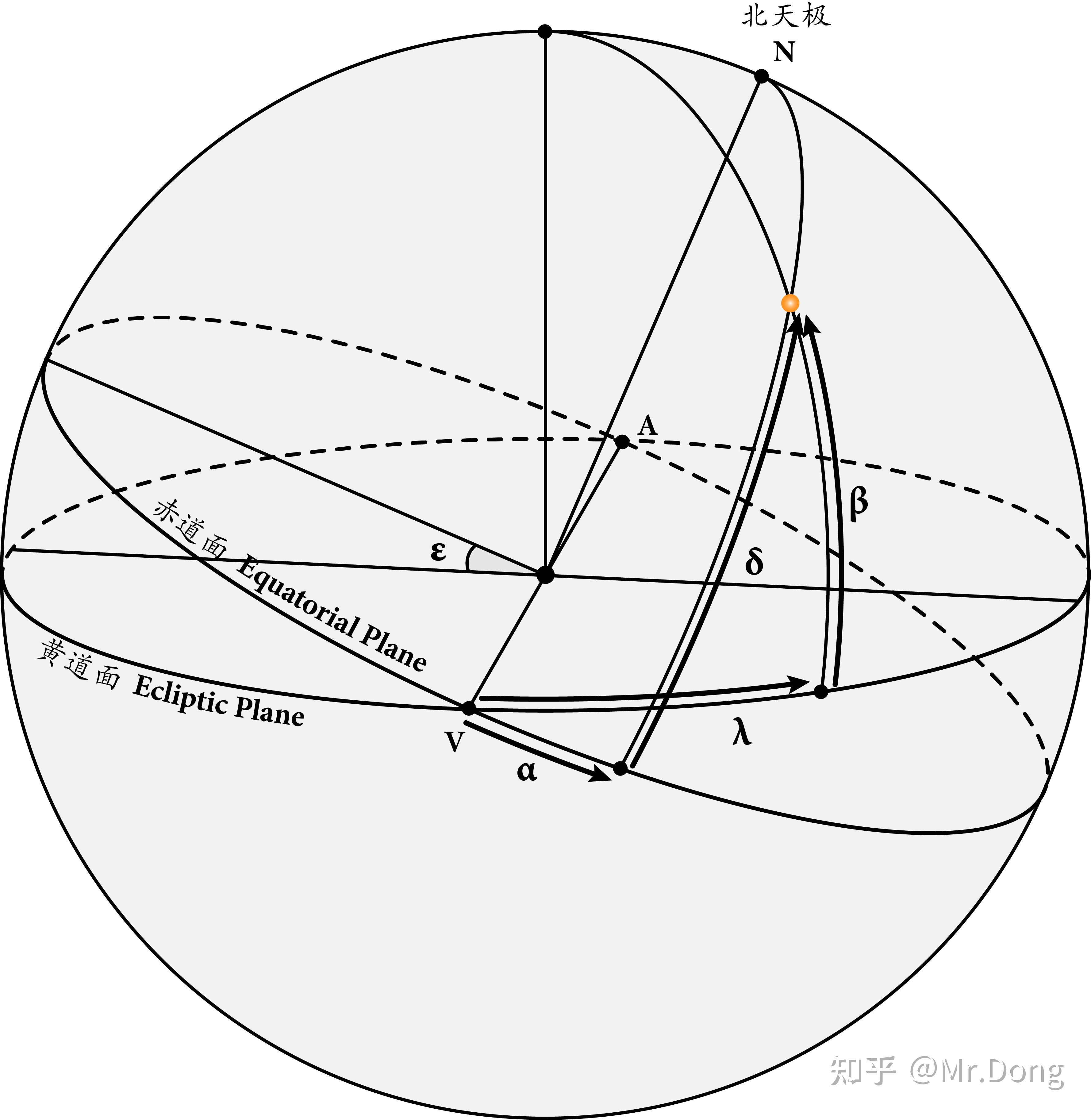
黄道坐标系到第二赤道坐标系

地平坐标系到时角坐标系
为了避免歧义，方程4中的φ继续用ψ代替
将黄道坐标系转换为第二赤道坐标系：
\begin{eqnarray}   \begin{cases}  \psi = \alpha - 90^\circ & \\   \psi' = \lambda-90^\circ &\\  \theta = 90^\circ - \delta &\\  \theta' = 90^\circ - \beta&\\  \chi = \epsilon&\\  \end{cases} \end{eqnarray}\tag{7.1}\\   
代入方程4
\begin{eqnarray}   \begin{cases}   \sin\lambda\cos\beta= \cos\delta\sin\alpha\cos\epsilon+\sin\delta\sin\epsilon & \\   \cos\lambda\cos\beta=\cos\alpha\cos\delta &\\  \sin\beta=\sin\delta\cos\epsilon-\sin\alpha\cos\delta\sin\epsilon\\   \end{cases} \end{eqnarray}\tag{7.2}\\   
将第二赤道坐标系转换为黄道坐标系：
\begin{eqnarray}   \begin{cases}  \psi = \lambda - 90^\circ & \\   \psi' = \alpha-90^\circ &\\  \theta = 90^\circ - \beta &\\  \theta' = 90^\circ - \delta&\\  \chi = -\epsilon&\\  \end{cases} \end{eqnarray}\tag{8.1}\\   
代入方程4
\begin{eqnarray}   \begin{cases}   \sin\alpha\cos\delta= \cos\beta\sin\lambda\cos\epsilon-\sin\beta\sin\epsilon & \\   \cos\alpha\cos\delta=\cos\lambda\cos\beta &\\  \sin\delta=\sin\beta\cos\epsilon+\sin\lambda\cos\beta\sin\epsilon\\   \end{cases} \end{eqnarray}\tag{8.2}\\   
<hr/>中天（Culmination）

中天是当天体正经过当地子午圈的时刻。中天又分为上中天（Upper Culmination）和下中天（Lower Culmination）；上中天是天体在最高点的位置（时角H=0h），也是其高度/地平纬度最大的时候（对于北半球），也就是最接近天顶的时刻；相反，下中天是天体在最低点的位置（时角H=12h），也是其高度/地平纬度最小的时候（对于北半球），也就是最接近天底的时刻。



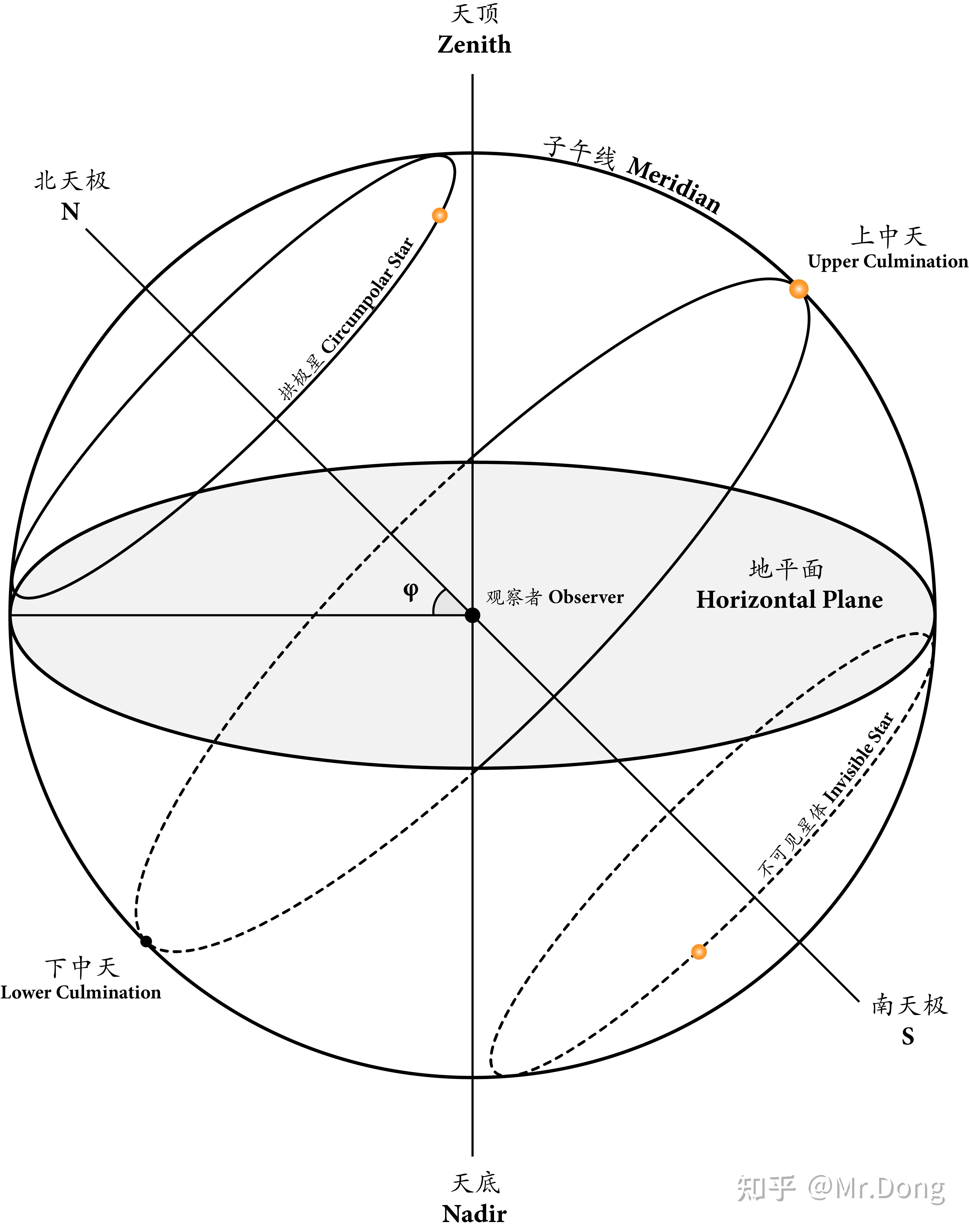
中天

我们现在只考虑在北半球的时候，南半球仅需要将 δ -> - δ 和 φ -> - φ 代入就好
我们现在将 H=0h 代入方程6.2中的最后一个：
\sin h =\sin\delta\sin\phi+\cos\delta\cos\phi\\
用三角函数恒等式化简可得：
\sin h =\sin\delta\sin\phi+\cos\delta\cos\phi=\cos(\phi-\delta)\\
因为 \cos\theta=\sin(90^\circ-\theta) ,继续化简：
\sin h =\cos(\phi-\delta)=\sin(90^\circ-\phi+\delta)\\
这个方程有两个根，所以我们可以得到
\boxed{h_u=\begin{eqnarray}   \begin{cases} 90^\circ - \phi+\delta & \\ 90^\circ+\phi-\delta &\\\end{cases} \end{eqnarray}}\tag{9}\\   
如果这个星体的上中天在天顶南面，那么 h_u=90^\circ - \phi+\delta  ;如果这个星体的上中天在天顶北面，那么 h_u=90^\circ + \phi-\delta 。
相同的，代入H=12h，我们现在可以得到下中天的高度：
\sin h =-\cos(\phi+\delta)=\sin(\phi+\delta-90^\circ)\\  
\boxed{h_l=\delta+\phi-90^\circ}\tag{10}

通过方程9和10，我们可以将所有的星体分成三类：

• 当 h_l>0 也就是当 \delta>90^\circ-\phi ，这个星体为拱极星（Circumpolar），也就永远不会落下，任何时刻都是在地平线以上
  
• 当 h_u<0 也就是当 \delta<\phi - 90^\circ ，这个星体为任何时刻都不可见
  
• 当 \phi-90^\circ<\delta<90^\circ-\phi 时，这个星体会升起并且落下
  

可以发现，当我们处在地球两极时，所有可以看到的星星都是拱极星，还有一半星体不可见；当我们在赤道时，所有星体都是升起并且落下，没有任何的拱极星或者不可见的星体。（由于大气折射，当δ = 90° - φ时也可以被看作为拱极星。）
在南半球我们只需要将 δ -> - δ 和 φ -> - φ 代入，所以当 δ < -(90° +  φ)时，星体为拱极星，当δ > 90° +  φ时，星体不可见。比如悉尼（φ=-34°），如果星体的赤纬δ<-56°时，其为拱极星，当星体的赤纬 δ > 56°时，星体不可见。
起落时间
我们将方程 \sin h=\sin\delta\sin\phi+\cos H\cos \delta\cos\phi 中的 \cos H 分离开来，就找到一个星体的起落时间:
\cos H = - \tan\delta\tan\phi+\frac{\sin h }{\cos\delta\cos\phi}\\
现在忽略大气折射，就可以将 h = 0 代入 （大气折射会增加视地平-34’），对于太阳和月亮这种天体还需要考虑其角半径；
\boxed{\cos H = -\tan\delta\tan\phi}\tag{11}\\
有了这个天体的赤纬和所在地区的纬度，我们就可以出其他在穿越地平线时的时角，也就可以找到升起和降落的时间。
<hr/>太阳 Sun

太阳的赤纬变化
用方程8.2的最后一个方程就可以得到太阳的赤纬。由于太阳在黄道面上，所以太阳的黄纬\beta_\odot 为0：
\sin\delta_\odot=\sin\epsilon\sin\lambda_\odot\\
并且如果忽略地球轨道的离心率，将其认为是一个完美的圆，太阳的黄经就为 \lambda_\odot=\frac{2\pi}{T_t} ;T_t 指的是回归年（Tropical Year）（与恒星年不一样），大约为365.24217太阳日，之后太阳的赤纬可以写成：
\boxed{\delta_\odot=\arcsin[\sin\epsilon\sin(\frac{2\pi}{T_t}t)]}\tag{12}



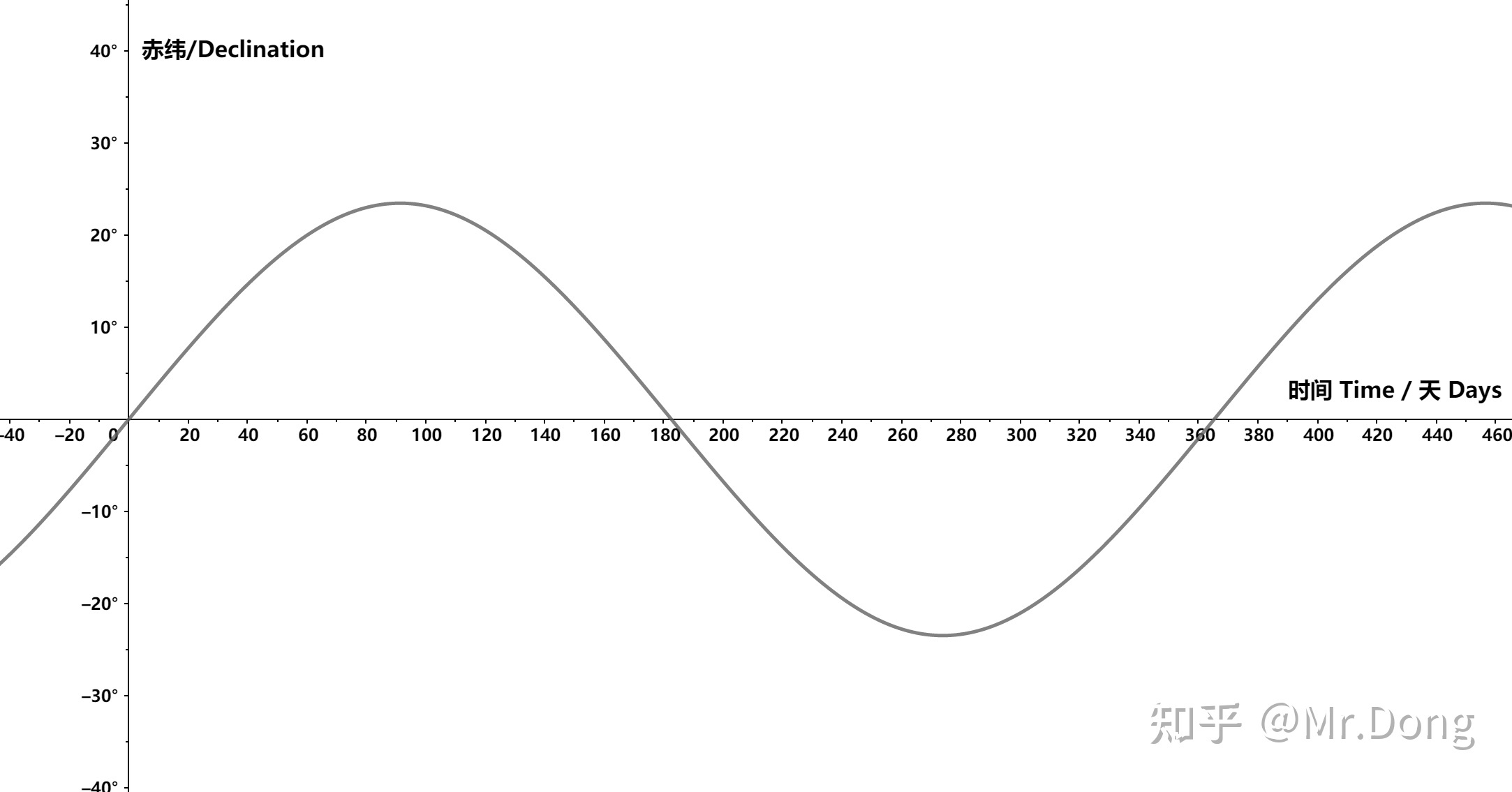
太阳赤纬 Declination of Sun

白昼时间
通过方程11，我们就可以找到太阳起落的时角，从而找到白昼的持续时间，太阳在地平线以上的时角为 2\arccos(-\tan{\delta_\odot\tan\phi}) ;因为 \cos(180^\circ-\theta)=-\cos\theta ，所以 \arccos(-\theta)=180^\circ-\arccos\theta 。现在我们将其转换为小时：
t_{day}=24^h\cdot[1-\frac{1}{180}\arccos(\tan\delta_\odot\tan\phi)]\tag{13}\\
可以发现，这个方程只在 \left| \tan\delta_\odot\tan\phi \right|\leq1 时才成立，如果 \left| \tan\delta_\odot\tan\phi \right|>1 时，太阳要不是是一直在地平线一下，或者是一直在地平线以上。
如果 \tan\delta_\odot\tan\phi>1 (北半球):
\tan\delta_\odot>\frac{1}{\tan\phi}\\ \tan\delta_\odot>\tan(90^\circ-\phi)\\ \delta_\odot>90^\circ-\phi\\
\delta_\odot>90^\circ-\phi 和北半球中拱极星的条件一样，所以当 \tan\delta_\odot\tan\phi>1 ，那么太阳将不会落下，也就是极昼。
同样的，当 \tan\delta_\odot\tan\phi<-1 时， \delta_\odot<\phi-90^\circ ，太阳将不会升起，也就是极夜。
对于南半球，条件也是一样。
<hr/>封面图像来自于悉尼大学 悉尼天文研究所 Sydney Institute for Astronomy
文中图像为我自己所做
推导和证明过程中可能有些小错误，如果有不对的地方可以联系我，或者直接在评论区评论，码字不易，希望大家多多支持，谢谢各位

涵涵爸爸520

想问一下文中图片的作图软件是什么？

分裂的硬盘悔

Adobe Illustrator

魏洋1

相当不错的天文科普文章[赞同]，不过文中提到的卡迪尔坐标应为笛卡尔坐标[思考]

用户5592359840

好！收藏了